Ensayo

1)forma normal de skolem

El punto álgido a la hora de encontrar la forma normal de Skolem de una fórmula es la eliminación de los cuantificadores existenciales, esta eliminación es conocida como skolemización. Las reglas básicas para realizar la skolemización son:

1. Si un cuantificador existencial no se encuentra dentro del ámbito de ningún cuantificador universal, se sustituye la variable cuantificada existencialmente por una constante que aún no haya sido utilizada y el cuantificador existencial es eliminado. La constante utilizada no puede volver a ser reutilizada. Por ejemplo, ${\displaystyle \exists xP(x)}$ puede ser cambiado a P(c), donde c es una nueva constante.
2. Si un cuantificador existencial se encuentra dentro del ámbito de un cuantificador universal, se ha de sustituir la variable cuantificada existencialmente por una función de la variable cuantificada universalmente y se elimina el cuantificador existencial. La función no puede haber sido utilizada previamente ni podrá utilizarse posteriormente. Por ejemplo, la fórmula ${\displaystyle \forall x\exists y\forall z.P(x,y,z)}$ no está en forma normal de Skolem porque ella contiene un cuantificador existencial ${\displaystyle \exists y}$. La skolemización reemplaza ${\displaystyle y}$ con ${\displaystyle f(x)}$, donde ${\displaystyle f}$ es una nuevo símbolo de función, y elimina la cuantificación existencial sobre ${\displaystyle y}$. La fórmula resultante es ${\displaystyle \forall x\forall z.P(x,f(x),z)}$. El término Skolem ${\displaystyle f(x)}$ contiene ${\displaystyle x}$ pero no ${\displaystyle z}$ porque el cuantificador a ser eliminado ${\displaystyle \exists y}$ está en el ámbito de ${\displaystyle \forall x}$ pero no en el ámbito de ${\displaystyle \forall z}$; debido a que la fórmula está en forma normal prenexa, esto es equivalente a decir que, en la aparición de los cuantificadores, ${\displaystyle x}$ precede ${\displaystyle y}$ mientras ${\displaystyle z}$ no. La fórmula obtenida por esta transformación es satifactible si y solo si la fórmula original lo es.
3. Si un cuantificador existencial se encuentra dentro del ámbito de más de un cuantificador universal se sustituirá la variable cuantificada existencialmente por una función de todas las variables afectadas por estos cuantificadores universales y se elimina el cuantificador existencial. La función no puede haber sido utilizada previamente ni podrá utilizarse posteriormente.

2)Sustitucion

En lógica, las reglas de reemplazo o reglas de sustitución son reglas de transformación que pueden ser aplicadas únicamente a un segmento particular de una expresión.

Un sistema lógico puede ser construido de manera que utilice axiomas, reglas de inferencia, o ambos, como reglas de transformación de expresiones lógicas en el sistema. Mientras que una regla de inferencia se aplica siempre a una expresión lógica general, una regla de reemplazo puede ser aplicada solamente a un segmento particular.

En el contexto de una prueba lógica, expresiones lógicamente equivalentes pueden sustituirse unas por otras. Las reglas de reemplazo se usan en la lógica proposicional para manipular proposiciones y efectuar estas sustituciones.

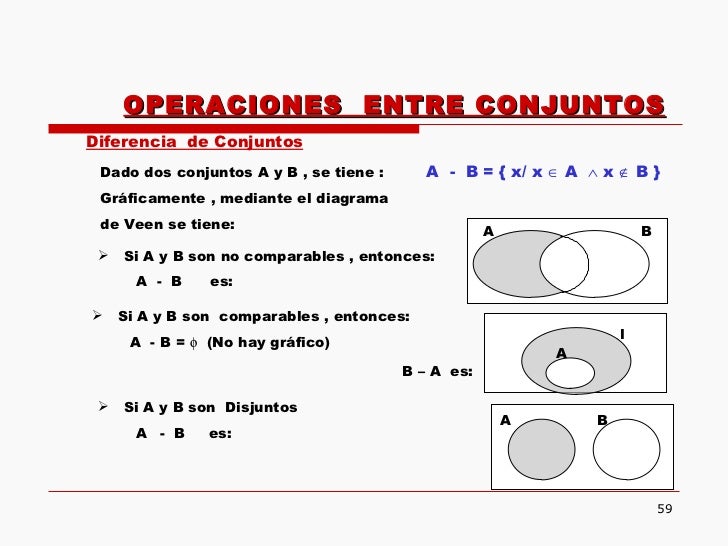
3)conjunto de diferencias

4)unificacion

Cuando se tienen sentencias compuestas por predicados y conectivos lógicos, se debe evaluar la veracidad de cada uno de sus componentes para determinar si toda la sentencia es verdadera o falsa. Para ello, se busca en el conjunto de axiomas la forma de establecer la veracidad de los predicados componentes. Un predicado componente se dice que es verdadero si se identifica con un axioma de la base de información. En la lógica de predicados, este proceso es algo complicado ya que las sentencias pueden tener términos variables. A los predicados que tienen variables por argumentos, se los denomina patrones.

La unificación es el proceso de computar las sustituciones apropiadas que permitan determinar si dos expresiones lógicas, ya sean predicados o patrones, coinciden.

El proceso de unificación involucra los siguientes pasos:

• Todo predicado que no contenga variables en sus argumentos, deben tener un axioma que se identifique totalmente, para considerarlo como verdadero.
• Si un predicado contiene una variable, esta debe ser asociada a un valor determinado. Esta asociación se realiza buscando en la base de axiomas y seleccionando todos aquellos que se identifican con el patrón en todo, excepto por la variable. La variable es asociada con el valor en la posición correspondiente del axioma. Si más de un axioma se identifica con el predicado dado, todos los valores asociados son considerados y son tratados separadamente.
• El proceso de identificación continua asumiendo que el valor de la variable es el valor asociado, en cualquier lugar que esta aparezca.
• Los conectivos lógicos son aplicados a todos los predicados, para determinar la veracidad de la sentencia dada.

5)Resolucion

Es una regla de inferencia utilizada sobre cierto tipo de proposiciones lógicas y es especialmente utilizada para los demostradores automatizados de teoremas. Utilizando resolución se puede construir un demostrador que sea completo (por contradicción) y correcto para la lógica proposicional y de primer orden supuesto que un conjunto de proposiciones son insatisfacción.